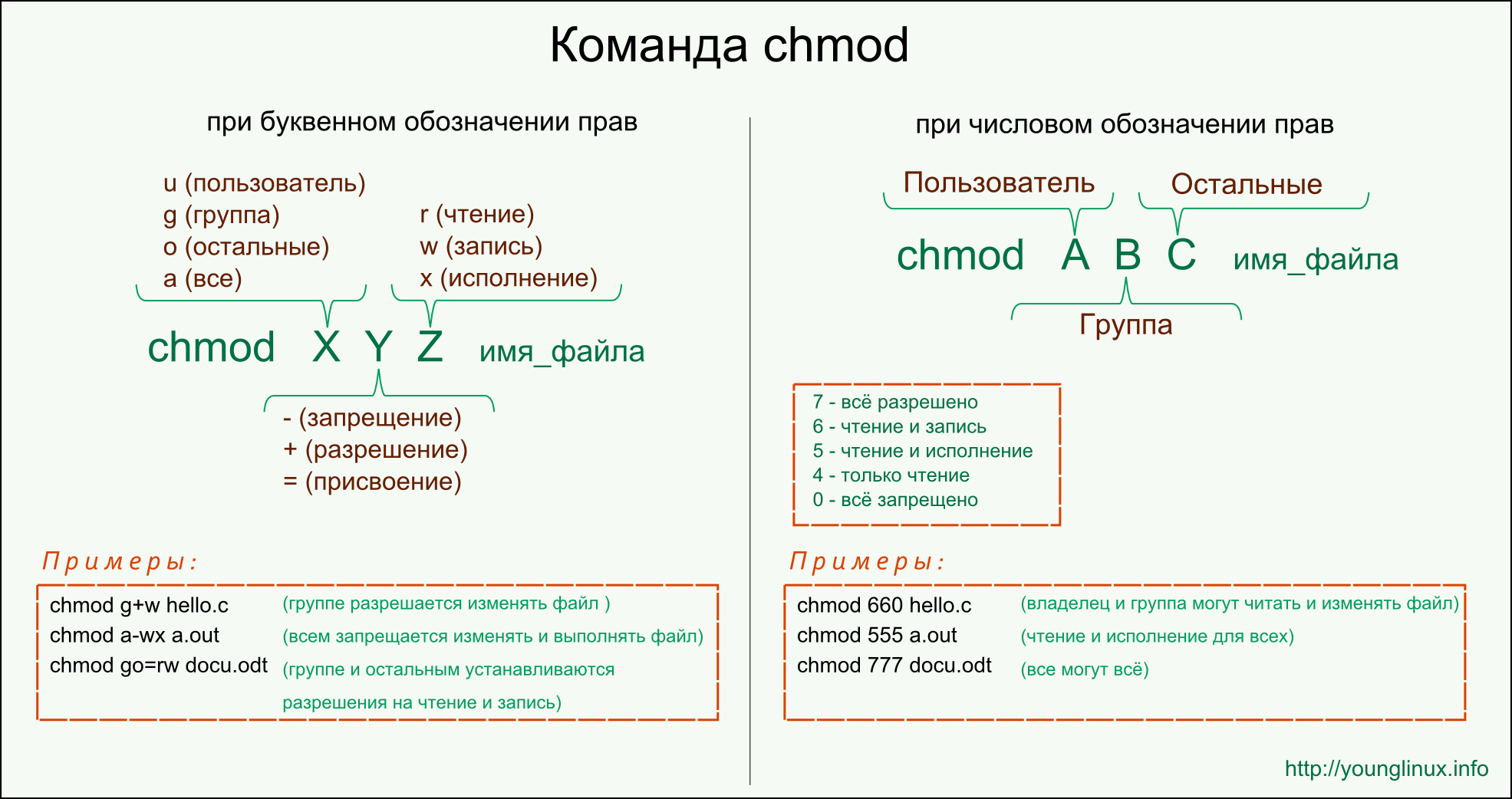
- Capacitated Vehicle Routing Problem (CVRP) with Python+Pulp and Google Maps API
- 1. Definition of the Problem
- 2. Which kind of model should we use?
- Vehicle Routing Problem
- NEO Research Group
- Capacitated VRP with Time Windows Instances
- Breedam
- Cordeau
- Solomon
- Homberger
- Russell
- Vehicle Routing Problem with Time Windows
- Overview
- VRPTW Example
- Solving the VRPTW example with OR-Tools
- Create the data
- Python
- Time callback
- Capacitated vehicle routing problem with time windows
- About
- Capacitated vehicle routing problem with time windows
- About
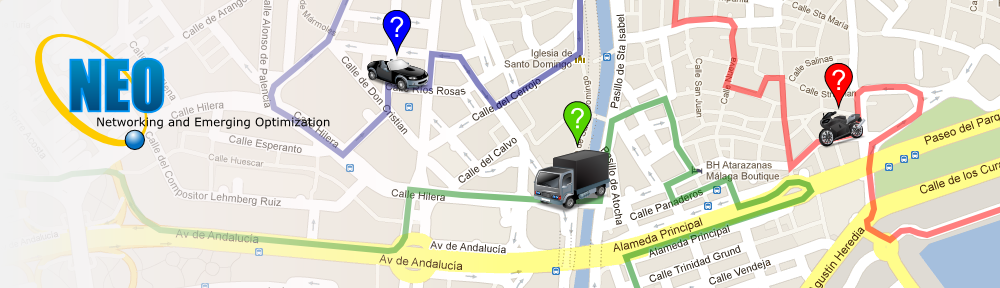
Capacitated Vehicle Routing Problem (CVRP) with Python+Pulp and Google Maps API
T he vehicle routing problem (VRP) is a combinatorial and integer programming which ask “What is the optimal set of routes for a fleet of vehicles in order to deliver to a given set of customers?” It generalizes the well-known traveling salesman problem (TSP).
There are many variants of vehicle routing problem. Some popular examples are as follows:
- CVRP (Capacitated Vehicle Routing Problem) : Vehicles have a limited carrying capacity of the goods that must be delivered.
- VRPTW (Vehicle Routing Problem with Time Windows) : The delivery locations have time windows within the deliveries (or visits) must be made.
- VRPPD (Vehicle Routing Problem with Pickup and Delivery) : A number of goods need to be moved from certain pickup locations to other delivery locations. The goal is to find optimal routes for a fleet of vehicles to visit the pickup and drop-off locations.
- VRPP (Vehicle Routing Problem with Profits) : It is a maximization problem where it is not mandatory for vehicles to visit all nodes. The aim is to visit nodes maximize the sum of collected profits under specific circumstances while respecting a given vehicle time limit. For example, assume there are two sets of customers, Ones are frequent customers that are mandatory for delivery, and another set is the non-frequent potential customers with known and estimated profits. Both sets have known demands and service requirements over a planning horizon of multiple days. The objective is to determine vehicles’ routes that maximize the net profit, while satisfying vehicles’ capacity, route duration and consistency constraints. Vehicles are required to start and end at the same depot.
In this post, I explain CVRP and show python+pulp based solution. The rest of this post is organized as follows:
- Definition of the Problem
- Which kind of model we should use?
- Formulate according to given constraints and model
- Coding with solver (Pulp)
- Visualization of results (Google Maps API)
1. Definition of the Problem
The capacitated vehicle routing problem (CVRP) is a VRP in which vehicles with limited carrying capacity need to pick up or deliver items to various locations. The items have a quantity, such as weight or volume, and each vehicle has a maximum capacity that they can carry. The problem is to pick up or deliver the items with the least cost, while never exceeding the capacity of the vehicles.
So, I will set a customer number, vehicle number, demand of each customer and capacity of vehicles as following.
- customer number : 9 (plus one depot)
- vehicle number : 4
- demand of each customer : random values between 10 to 20
- vehicle capacity : 50 (assume that all vehicles have the same capacity)
2. Which kind of model should we use?
Graph theory is often used (numerical data is added to nodes and edges of graphs) for the vehicle routing problems. This is because it is possible to think in a way that selecting (or not selecting) routes by passing (or not passing) edges. In this context, assigning ‘1’ to an edge means that a route is being selected. Yes! It can be said that this corresponds to the integer optimization problem. This post will also explain the CVRP problem using a graph.
Vehicle Routing Problem
NEO Research Group
Capacitated VRP with Time Windows Instances
The best known solutions for most of these benchmarks can be found here.
Breedam
Click here to see the structure of Breedam files.
- Vehicles with capacity equal to 100 (T1 60 files, T2 60 files)
Cordeau
The structure of these files is described here.
Solomon
The structure of these files is described here.
Homberger
The orginal 56 Vehicle Routing Problems with Time Windows (VRPTW) instances designed by Prof. Marius M. Solomon in 1983 contain 100 customers. Here, a large set of new instances with 200, 400, 600, 800 and 1000 customers is presented. Description of the extended SOLOMON’s instances is specified here.
These instances are divided into three categories : C-type (clustered customers), R-type (uniformly distributed customers) and RC-type (a mix of R and C types); and we have instances of 200, 400, 600, 800 and 1000 customers for each category.
| Customers | Type C1 | Type C2 | Type R1 | Type R2 | Type RC1 | Type RC2 |
|---|---|---|---|---|---|---|
| 200 | S-C1-200 | S-C2-200 | S-R1-200 | S-R2-200 | S-RC1-200 | S-RC2-200 |
| 400 | S-C1-400 | S-C2-400 | S-R1-400 | S-R2-400 | S-RC1-400 | S-RC2-400 |
| 600 | S-C1-600 | S-C2-600 | S-R1-600 | S-R2-600 | S-RC1-600 | S-RC2-600 |
| 800 | S-C1-800 | S-C2-800 | S-R1-800 | S-R2-800 | S-RC1-800 | S-RC2-800 |
| 1000 | S-C1-1000 | S-C2-1000 | S-R1-1000 | S-R2-1000 | S-RC1-1000 | S-RC2-1000 |
Russell
The set of instances of Russell is composed of two real-world instances, and it was originally proposed in [Russell 1995].
The best-known solutions for this benchmark are published in [Mester & Bräysy 2005].
Vehicle Routing Problem with Time Windows
Overview
Many vehicle routing problems involve scheduling visits to customers who are only available during specific time windows. These problems are known as vehicle routing problems with time windows (VRPTWs).
VRPTW Example
On this page, we’ll walk through an example that shows how to solve a VRPTW. Since the problem involves time windows, the data include a time matrix, which contains the travel times between locations (rather than a distance matrix as in previous examples).
The diagram below shows the locations to visit in blue and the depot in black. The time windows are shown above each location. See Location coordinates in the VRP section for more details about how the locations are defined.
The goal is to minimize the total travel time of the vehicles.
Solving the VRPTW example with OR-Tools
The following sections describe how to solve the VRPTW example with OR-Tools.
Create the data
The following function creates the data for the problem.
Python
The data consists of:
- data[‘time_matrix’] : An array of travel times between locations. Note that this differs from previous examples, which use a distance matrix. If all vehicles travel at the same speed, you will get the same solution if you use a distance matrix or a time matrix, since travel distances are a constant multiple of travel times.
- data[‘time_windows’] : An array of time windows for the locations, which you can think of as requested times for a visit. Vehicles must visit a location within its time window.
- data[‘num_vehicles’] : The number of vehicles in the fleet.
- data[‘depot’] : The index of the depot.
The data consists of:
- time_matrix : An array of travel times between locations. Note that this differs from previous examples, which use a distance matrix. If all vehicles travel at the same speed, you will get the same solution if you use a distance matrix or a time matrix, since travel distances are a constant multiple of travel times.
- time_windows : An array of time windows for the locations, which you can think of as requested times for a visit. Vehicles must visit a location within its time window.
- num_vehicles : The number of vehicles in the fleet.
- depot : The index of the depot.
The data consists of:
- timeMatrix : An array of travel times between locations. Note that this differs from previous examples, which use a distance matrix. If all vehicles travel at the same speed, you will get the same solution if you use a distance matrix or a time matrix, since travel distances are a constant multiple of travel times.
- timeWindows : An array of time windows for the locations, which you can think of as requested times for a visit. Vehicles must visit a location within its time window.
- vehicleNumber : The number of vehicles in the fleet.
- depot : The index of the depot.
The data consists of:
- TimeMatrix : An array of travel times between locations. Note that this differs from previous examples, which use a distance matrix. If all vehicles travel at the same speed, you will get the same solution if you use a distance matrix or a time matrix, since travel distances are a constant multiple of travel times.
- TimeWindows : An array of time windows for the locations, which you can think of as requested times for a visit. Vehicles must visit a location within its time window.
- VehicleNumber : The number of vehicles in the fleet.
- Depot : The index of the depot.
Time callback
The following function creates the time callback and passes it to the solver. It also sets the arc costs, which define the cost of travel, to be the travel times between locations.
Capacitated vehicle routing problem with time windows
Capacitated Vehicle Routing Problem with Time Windows — розв’язок проблеми оптимізації руху із врахуванням вмістимості транспортних засобів та часовими обмеженнями за допомогою OR-Tools
- відкрийте діалогове вікно виконання команд win + R
- відкрийте термінал, введіть cmd
- перейдіть в папку з RabbitMQ cd C:\Program Files\RabbitMQ Server\rabbitmq_server-***\sbin
- запускаємо сервіс rabbitmq-service.bat start
- при потребі переходимо на management сторінку http://localhost:15672, логін та пароль — guest
- відкрийте діалогове вікно виконання команд win + R
- відкрийте термінал, введіть cmd
- перейдіть в папку з OR-Tools cd **\CVRPTW\backend\OR-Tools
- будуємо проект dotnet build
- запускаємо сервіс dotnet run —project OR-Tools
- відкрийте діалогове вікно виконання команд win + R
- відкрийте термінал, введіть cmd
- перейдіть в папку з API cd **\CVRPTW\backend\API
- будуємо проект dotnet build
- запускаємо сервіс dotnet run —project API
- документація — http://localhost:5000/swagger/index.html
- відкрийте діалогове вікно виконання команд win + R
- відкрийте термінал, введіть cmd
- перейдіть в папку з клієнтом cd **\CVRPTW\frontend\Angular
- встановлюємо пакети npm install
- запускаємо сервіс ng serve
- відкриваємо аплікацію — http://localhost:4200
Запуск за допомогою Docker
- відкривайте Docker Terminal
- перейдіть в папку проекту cd **\CVRPTW
- будуємо проект docker-compose build
- запускаємо сервіси docker-compose up -d
На Windows сервіси можуть бути доступні за іншою адресою. Щоб її дізнатись введіть docker-machine ip

About
Capacitated Vehicle Routing Problem with Time Windows
Capacitated vehicle routing problem with time windows
Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) solver
Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) solver written in Python.
This program solves Capacitated Vehicle Routing Problem with Time Windows (CVRPTW).
For example, given the following network and three vehicles at the depot (node 0) to pick up all demands on all nodes in as short a time period as possible,
the program provides the solution as follows:
Python 3.8 or later is required.
First, install the dependencies:
Alternatively, if you have pipenv installed, run the following commands instead of the second to fourth line above:
Then, let’s solve a sample problem!
It should output the solution as follows:
In addition, if you want to export images of the network and routes, use -g/—graph option:
It also generates network.png and route.png for vizualizing the network and the routes of vehicles.
data.sample.yaml is just sample data of a problem, so if you want to solve your own, copy data.sample.yaml and create your own data.yaml ! 💪
About
Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) solver written in Python.